6本組木は Bill Cutler によって詳しく解析されている。
以下は私による解析。
6本組木は Bill Cutler によって詳しく解析されている。
以下は私による解析。
次の表で、駒組がふたつある場合、下段の駒組は鏡像。
| Name | Pieces | Holes | Length | Sols | Moves | Col | Designer | Inv | Remark |
|---|---|---|---|---|---|---|---|---|---|
| Wyatt #3 | 0 51 187 1023×3 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #6 | 0 51 255 927 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #15 | 0 51 255 1023×3 | 2 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #13 | 0 51 823 1023×3 | 1 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| 0 51 974 1023×3 | |||||||||
| Wyatt #8 | 0 102 255 927 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Solid Burr in a Cage | 0 119 870 959 991 1023 | 0 | 6+ | 3 / 3 | 1.2 max | 1 | 私 (me) | 2003 | |
| + Cage Type-3 | 6 | 2 / 3 | 1.3.2.4.2.2 | ||||||
| 8 | 1.3.2.6 | ||||||||
| Impossible Second Move | 0 231 1023×2 1935×2 | 2 | 6+ | 1 / 1 | 1.2 | 1 | Bill Cutler | ||
| 0 126 1023×2 2847×2 | |||||||||
| Wyatt #5 | 0 153 255×2 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #7 | 0 153 870 1023×3 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #4 | 0 187 255×2 927 1023 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #14, #17 | 0 187 255×2 1023×2 | 2 | 6+ | 2 / 2 | 1 | 1 | 1956 | [2] | |
| 6+6=CUBE | 0 187 255 791 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 北島孝二 (Koji Kitajima) | 1993 | |
| 0 187 255 910 1023×2 | |||||||||
| 山中組木セット 黒 | 0 187 255 959 974 1023 | 0 | 6+ | 2 / 2 | 1.2 max | 1 | |||
| 0 187 255 823 991 1023 | |||||||||
| Wyatt #16 | 0 187 255 823 1023×2 | 1 | 6+ | 2 / 2 | 1 | 1 | 1956 | [2] | |
| 0 187 255 974 1023×2 | |||||||||
| 山中組木セット 橙 | 0 187 870 927 1023×2 | 0 | 6+ | 1 / 1 | 1.2 | 1 | |||
| 6+6=CUBE 改 | 0 255 910 959 974 1023 | 0 | 6+ | 1 / 1 | 1 | 1 | 私 (me) | 2007 | |
| 0 255 791 823 991 1023 | |||||||||
| Wyatt #1 | 0 255 823 927 974 1023 | 0 | 6+ | 2 / 2 | 1 | 1 | 1956 | [2] | |
| Burr in a Cage 1.18 | 0 479 511 910 959 1023 | 2 | 6 | 8 / 8 | 1.2 max | 1 | 私 (me) | 2003 | |
| 0 703 767 791 991 1023 | |||||||||
| + Cage Type-3 | 1 / 8 | 1.18.2.4.2 | |||||||
| Caged Notchable Unique 1.11 Moves 5 Holes | 0 511 887 959×2 1023 | 5 | 6 | 6 / 6 | 1.2 max | 1 | 私 (me) | 2002 | |
| 0 767 991×2 1006 1023 | |||||||||
| + Cage Type-2 | 13 | 1 / 10 | 1.11.2.3 | ||||||
| Wyatt #2 | 0 791 823 974 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| 0 823 910 974 1023×2 | |||||||||
| Different at Lengths 10 & 12 | 15 767×2 884 927 1007 | 5 | 10 | 1 / 1 | 5.3 | 1 | Bruce Love | 1987 | |
| 15 511×2 895 927 994 | |||||||||
| Wyatt #12 | 17 51 102 1023×3 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| Wyatt #10 | 17 51 255×2 791 1023 | 0 | 6+ | 2 / 2 | 1 | 1 | 1956 | [2] | |
| 17 51 255×2 910 1023 | |||||||||
| 山中組木セット 緑 | 17 51 870 927 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | |||
| Puzzle A | 19 115 511 831 910 1023 | 1 | 6+ | 3 / 4 | 3 max | 1 | Lester Henderson | ||
| 49 55 767 791 975 1023 | |||||||||
| Abad's Level 3 Burr 1 Hole | 23 119 157 191 991 1023 | 1 | 6+ | 1 / 12 | 3 | 1 | Rafael G. Abad | 2007 | |
| 113 119 155 223 959 1023 | |||||||||
| Puzzle #12 | 113 191 511 867 959 991 | 4 | 6 | 2 / 7 | 6.2 max | 1 | Derwin F. Brown | ||
| 23 223 767 867 959 991 | |||||||||
| Snapped Burr | 25 255 1023×2 4511 4919 | - | 6 | - | - | 1 | Yavuz Demirhan | 2017 | |
| 137 255 1023×2 4471 8863 | |||||||||
| + Frame | 7 | 1 / 12 | 6.6.3 | ||||||
| A Challenge for Wall Street | 143 687 989 1015 1023×2 | 9 | 6 | 40 / 43 | 4 max | 1 | Logan Kleinwaks | 2014 | max moves unique with Cage Type-3 |
| 31 351 955 1022 1023×2 | |||||||||
| + Cage Type-3 | 1 / 43 | 29.3.3.3 | |||||||
| Abad's Level 5.7 Improved Burr | 31 475 631 823 955 1023 | 4 | 6+ | 1 / 11 | 5.7 | 1 | Rafael G. Abad | 2006 | |
| 143 494 701 974 989 1023 | |||||||||
| Twist Burr | 34 157 511 984 (1006) (1023) | 0 | 6+ | 1 / 1 | 4.2 | 1 | William Meek | [R] |
|
| 34 155 767 (887) 945 (1023) | |||||||||
| Second Design | 35 511 799 910 972 1023 | 1 | 6+ | 1 / 1 | 3 | 1 | Victor Goedicke | ||
| 50 767 791 819 911 1023 | |||||||||
| とても難しい組木 | 70 119 870 927 991 1023 | 2 | 6+ | 1 / 10 | 4.2 | 1 | Edward Hordern? | ||
| 38 119 870 927 959 1023 | |||||||||
| Interrupted Slide | 46 111 735 759 955 1023 | 4 | 6 | 2 / 9 | 3.2.2 | 1 | Stewart T. Coffin | ||
| 71 111 447 510 989 1023 | 6+ | 3 | |||||||
| Love's B4 | 46 479 703 924 999 1023 | 4 | 6+ | 1 / 3 | 5 | 1 | Bruce Love | ||
| 71 479 703 894 915 1023 | |||||||||
| Wyatt #9 | 51×2 102 927 1023×2 | 0 | 6+ | 1 / 1 | 1 | 1 | 1956 | [2] | |
| 山中組木セット 黄 | 51×2 255 791 927 1023 | 0 | 6+ | 1 / 1 | 1 | 1 | |||
| 51×2 255 910 927 1023 | |||||||||
| BB31-10-40 | 51 117 787 959 1006 1023 | 1 | 6+ | 1 / 2 | 3 | 1 | Bill Cutler | ||
| 51 87 887 908 991 1023 | |||||||||
| 6+6=CUBE | 51 102 119 927 959 991 | 0 | 6+ | 1 / 1 | 1 | 1 | 北島孝二 (Koji Kitajima) | 1993 | |
| Wyatt #11 | 51 153 255×2 791 1023 | 0 | 6+ | 0 / 1 | 1 | 1956 | [2] | ||
| 51 153 255×2 910 1023 | |||||||||
| Burrloop | 51 255×3 1023×2 | 8 | 6 | 5 / 5 | 3 max | 1 | Yavuz Demirhan | 2016 | |
| + Cage | 1 / 16 | 7 | |||||||
| Caged Notchable Unique 4.12 Moves 9 Holes | 51 255 511 887 1023×2 | 9 | 6 | 36 / 44 | 3 max | 1 | 私 (me) | 2002 | |
| 51 255 767 1006 1023×2 | |||||||||
| + Cage Type-2 | 17 | 1 / 143 | 4.12.2.1.2.2 | ||||||
| Burr in a Cube | 51 255 887 1006 1023×2 | 8 | 6 | 20 / 20 | 2 max | 1 | Jürg von Känel | ||
| + Cage Type-1 | 2 / 52 | 4.6.3.4 | |||||||
| 6+6=CUBE 改 | 51 358 823 870 927 1023 | 0 | 6+ | 1 / 1 | 1 | 1 | 私 (me) | 2007 | |
| 51 614 870 927 974 1023 | |||||||||
| Burr #306 | 51 358 823 870 959 991 | 0 | 6+ | 1 / 1 | 1 | 1 | Unknown | ||
| 51 614 870 959 974 991 | |||||||||
| Burr #305 | 51 358 823 910 959 991 | 0 | 6+ | 1 / 1 | 1 | 1 | Bill Cutler | ||
| 51 614 791 959 974 991 | |||||||||
| BC L6000 | 99 187 447 895 927 1023 | 5 | 6 | 2 / 25 | 6.4 max | 1 | Bruno Curfs | ||
| 54 187 735 927 1007 1023 | |||||||||
| Puzzle #23 | 99 363 511 765 991 1015 | 5 | 6 | 1 / 9 | 6 | 1 | Derwin F. Brown | ||
| 54 507 621 767 959 1022 | |||||||||
| Triple Slide | 115 157 171 479 895 1023 | 2 | 6+ | 1 / 1 | 3 | 1 | Stewart T. Coffin | ||
| 55 93 155 703 1007 1023 | |||||||||
| BC UL7000 | 199 507 703 767 1007 1020 | 7 | 6 | 1 / 16 | 7.2 | 1 | Bruno Curfs | ||
| 62 479 511 765 895 1011 | |||||||||
| jvk #25.2 derivation | 85 191 505 959 979 1022 | 3 | 6+ | 1 / 2 | 3 | 1 | Jürg von Känel | ||
| 85 223 761 956 991 1015 | |||||||||
| jvk #25.2 | 85 255 791 927 959 1023 | 5 | 6+ | 1 / 14 | 3 | 1 | Jürg von Känel | ||
| 85 255 910 927 991 1023 | |||||||||
| Modification of Burr 'B' | 117 159 511 767 895 959 | 7 | 6 | 13 / 40 | 10 max | 1 | Edward Hordern | ||
| 87 159 511 767 991 1007 | |||||||||
| Love's Dozen | 117 479 767 895 959 991 | 9 | 6 | 90 / 154 | 12.3 max | 1 | Bruce Love | 1987 | max moves |
| 87 511 703 959 991 1007 | |||||||||
| Love's Sweet Sixteen | + Cage | 9 | 6 | 1 / 96 | 16 | 3 | Tyler Hudson | 2022 | |
| Burr 'B' (Piston Puzzle Burr) | 117 511 767 895×2 921 | 7 | 6 | 1 / 10 | 9.3 | 1 | Peter Marineau | 1986 | max moves unique 6-len |
| 87 511 767 921 1007×2 | |||||||||
| Millable 5.4 Moves 2 Holes #2 | 102 159×2 191 991 1023 | 2 | 6 | 2 / 2 | 5.4 | 1 | 私 (me) | 2002 | |
| 102 159×2 223 959 1023 | |||||||||
| Millable 5.4 Moves 2 Holes #1 | 102 159 191 927 974 1023 | 2 | 6 | 2 / 2 | 5.4 | 1 | 私 (me) | 2002 | |
| 102 159 223 823 927 1023 | |||||||||
| jvk #25.1 | 102 187 255 823 927 1023 | 3 | 6 | 1 / 7 | 5.2 | 1 | Jürg von Känel | ||
| 102 187 255 927 974 1023 | |||||||||
| Caged Notchable Unique 6 Moves 9 Holes #1 | 102 255 375 767 959 991 | 6 | 6 | 2 / 16 | 3 | 1 | 私 (me) | 2002 | |
| 102 255 511 750 959 991 | |||||||||
| + Cage Type-3 | 1 / 16 | 6.1.2.4.2 | |||||||
| jvk's favorite notchable burr | 102 255 669 927 974 1023 | 3 | 6 | 1 / 4 | 5.4 | 1 | Jürg von Känel | co-max moves unique notchable 6-len 3-holes | |
| 102 255 411 823 927 1023 | |||||||||
| Caged Notchable Unique 6.5 Moves 9 Holes | 102 255 511 1006 1023×2 | 9 | 6 | 17 / 24 | 3 max | 1 | 私 (me) | 2002 | |
| 102 255 767 887 1023×2 | |||||||||
| + Cage Type-1 | 1 / 72 | 6.5.1.2.2.3 | |||||||
| Favorite Level 5.4 Millable Burr | 102 765×2 927 974 1023 | 5 | 6 | 1 / 3 | 5.4 | 1 | David V. Winkler | ||
| 102 507×2 823 927 1023 | |||||||||
| Bill's Baffling Burr (BBB) | 102 510 892 959 991 1023 | 7 | 6 | 1 / 24 | 5 | 1 | Bill Cutler | 1984 | |
| 102 759 959 991 995 1023 | |||||||||
| Notchable 5 Moves 2 Holes | 119 153×2 255 1023×2 | 2 | 6 | 2 / 4 | 5.4 max | 1 | 私 (me) | 2002 | |
| Clasped Burr #2 | 119 153 255×3 1023 | 4 | 6 | 1 / 3 | 2 | 1 | Yavuz Demirhan | 2016 | |
| + Cage | 1 / 16 | 4.2.2.2 | |||||||
| Notchable Unique 5 Moves 3 Holes #2 | 119 153 255 411 959 1023 | 3 | 6 | 1 / 8 | 5.4 | 1 | 私 (me) | 2002 | co-max moves unique notchable 6-len 3-holes |
| 119 153 255 669 991 1023 | |||||||||
| Abad's Level 5.4 Burr | 119 155 157 191 991 1023 | 2 | 6 | 1 / 22 | 5.4 | 1 | Rafael G. Abad | 2006 | |
| 119 155 157 223 959 1023 | |||||||||
| Gaby Games | 119 159 255 767 879 991 | 6 | 6 | 1 / 2 | 6.4 | 1 | Philippe Dubois | ||
| 119 159 255 511 879 959 | |||||||||
| Notchable Unique 3 Moves 2 Holes #2 | 119 187 275 910 1023×2 | 2 | 6+ | 1 / 2 | 3 | 1 | 私 (me) | 2002 | |
| 119 187 652 791 1023×2 | |||||||||
| Favorite Level 5.4 Notchable Burr | 119 187 411 927 959 1023 | 5 | 6 | 1 / 24 | 5.4 | 1 | David V. Winkler | ||
| 119 187 669 927 991 1023 | |||||||||
| Notchable 2 Moves 1 Hole #3 | 119 187 791 823 910 1023 | 1 | 6+ | 2 / 2 | 2 | 1 | 私 (me) | 2002 | |
| 119 187 791 910 974 1023 | |||||||||
| Notchable Unique 3 Moves 2 Holes #1 | 119 187 791 887 1023 1932 | 2 | 6+ | 1 / 1 | 3 | 1 | 私 (me) | 2002 | |
| 119 187 910 1006 1023 2835 | |||||||||
| Burr in a Cage 5.17 | 119 191 255 507 767 1023 | 8 | 6 | 72 / 192 | 2.2 max | 1 | 私 (me) | 2003 | |
| 119 223 255 511 765 1023 | |||||||||
| + Cage Type-3 | 1 / 192 | 5.17.4.2.2 | |||||||
| Solid Puzzle No.3 | 119 255×4 1023 | 8 | 6 | 1 / 1 | 2 | 1 | テンヨー (Tenyo) | ||
| Caged Notchable Unique 6 Moves 9 Holes #2 | 119 375 767 870 959 991 | 6 | 6 | 2 / 8 | 3 | 1 | 私 (me) | 2002 | |
| 119 511 750 870 959 991 | |||||||||
| + Cage Type-3 | 1 / 8 | 6.1.2.4.2 | |||||||
| Burr in a Cage 5.11 | 119 479×2 631 1023×2 | 9 | 6 | 10 / 16 | 2.2 max | 1 | 私 (me) | 2003 | |
| 119 494 703×2 1023×2 | |||||||||
| + Cage Type-3 | 1 / 16 | 5.11.4.6.2.2 | |||||||
| 1 Hole L2 Notchable | 119 791 823 910 959 974 | 1 | 6+ | 4 / 4 | 2 max | 1 | Bill Cutler | 1987 | |
| 119 791 823 910 974 991 | |||||||||
| Vertex Burr #1 | 215 255 495 1006 1023×2 | 10 | 6 | 5 / 6 | 2 max | 1 | Yavuz Demirhan | 2012 | |
| 125 255 639 887 1023×2 | |||||||||
| + Cage Type-4 | 11 | 1 / 30 | 12 | ||||||
| Improved Burr | 215 358 927 942 972 1023 | 2 | 6+ | 1 / 1 | 2.3 | 1 | Stewart T. Coffin | ||
| 125 614 819 855 927 1023 | |||||||||
| Burr 'A' | 126 495 735 895 959 989 | 8 | 6+ | 2 / 9 | 5 max | 1 | Peter Marineau | ||
| 231 447 639 955 991 1007 | |||||||||
| Two Against One | 223 239 767×2 895 1023 | 11 | 6 | 16 / 16 | 3 max | 2 | Logan Kleinwaks | 2015 | max moves with Cage Type-3 |
| 127 191 511×2 1007 1023 | |||||||||
| + Cage Type-3 | 1 / 16 | 32.2.1.2 | |||||||
| Pruts | 127 487 735 767 911 991 | 7 | 6 | 1 / 6 | 7 | 1 | Alfons Eyckmans | 2023 | |
| 239 447 511 638 799 959 | |||||||||
| Burred Box | 127 495 511 767 1022 1023 | 12 | 6 | 1 / 1 | 3 | 2 | William Hu | 2014 | |
| 239 511 639 767 1015 1023 | |||||||||
| + 8/3501 | 4 | 1 / 1 | 7 | ||||||
| Love's Model | 127 496 671 989 1015 1023 | 6 | 6 | 1 / 7 | 7 | 1 | Bruce Love | ||
| 239 415 496 955 1022 1023 | |||||||||
| Notchable 9 Moves 7 Holes | 153 343 511 1006 1023×2 | 7 | 6 | 16 / 26 | 9.2 max | 1 | 私 (me) | 2002 | max moves notchable 6-len |
| 153 686 767 887 1023×2 | |||||||||
| Notchable Unique 2.5 Moves 4 Holes | 153 343 703 959 991 1006 | 4 | 6+ | 1 / 1 | 2.5 | 1 | 私 (me) | 2002 | |
| 153 479 686 887 959 991 | |||||||||
| L46AA Notchable | 153 479 494 1023×3 | 9 | 10+ | 36 / 56 | 10 max | 1 | Bill Cutler | 1987 | |
| 8 | 36 / 56 | 6 max | |||||||
| 153 631 703 1023×3 | |||||||||
| 6 | 44 / 56 | 5.2 max | |||||||
| BC UL5000 | 155 511 935 959 974 1020 | 5 | 6 | 1 / 6 | 5.6 | 1 | Bruno Curfs | ||
| 157 767 823 862 991 1011 | |||||||||
| Variation of Gaby Games | 159×2 255 767 879 991 | 6 | 6 | 3 / 3 | 5.4 max | 1 | Richard Korsmeyer | ||
| 159×2 255 511 879 959 | |||||||||
| Millable Unique 5.4.2 Moves 4 Holes | 159 187 375 669 991 1023 | 4 | 6 | 1 / 16 | 5.4.2 | 1 | 私 (me) | 2002 | |
| 159 187 411 750 959 1023 | |||||||||
| Abad's Level 5 Most Assemblies Burr | 159 223 511 703 767 989 | 7 | 8+ | 1 / 896 | 5 | 1 | Rafael G. Abad | 2006 | |
| 159 191 479 511 767 955 | |||||||||
| Burr in a Cage 9.16 | 159 191 479 974 1023×2 | 8 | 6 | 80 / 164 | 4.2 max | 1 | 私 (me) | 2003 | |
| 159 223 703 823 1023×2 | |||||||||
| + Cage Type-3 | 1 / 164 | 9.16.3.3.2 | |||||||
| Burrow | 159 191 599 959 975×2 | 4 | 6 | 1 / 3 | 2.2 | 1 | Stephan Baumegger | 2014 | |
| 159 223 430 831×2 991 | |||||||||
| + 3 Frames | 1 / 3 | 17.3.4.3.2 | |||||||
| Caged Millable Unique 7.15 Moves 8 Holes | 159 191 735 974 1023×2 | 8 | 6 | 80 / 164 | 4.2 max | 1 | 私 (me) | 2003 | |
| 159 223 447 823 1023×2 | |||||||||
| + Cage Type-3 | 1 / 164 | 7.15.3.3.2 | |||||||
| Caged Millable 19.15 Moves 10 Holes | 159 191 767 887 1023×2 | 10 | 6 | 229 / 304 | 4 max | 1 | 私 (me) | 2003 | |
| 159 223 511 1006 1023×2 | |||||||||
| + Cage Type-3 | 47 / 304 | 19.15.3.4.2 max | |||||||
| Abad's Level 9 Burr | 159 378 447 511 765 1014 | 5 | 6 | 1 / 2 | 9 | 1 | Rafael G. Abad | 2006 | |
| 159 507 735 741 767 1014 | |||||||||
| Computer's Choice 5-Hole | 159 511 756 767 923 1014 | 5 | 6+ | 1 / 7 | 9 | 1 | Bill Cutler | 1988 | |
| 159 498 511 767 925 1014 | |||||||||
| Notchable Unique 5 Moves 3 Holes #3 | 187 255 326 927 974 1023 | 3 | 6 | 1 / 5 | 5.2 | 1 | 私 (me) | 2002 | |
| 187 255 550 823 927 1023 | |||||||||
| L5 Notchable Most Assemblies | 187 255 411 767×2 1023 | 8 | 10+ | 1 / 480 | 5 | 1 | Bill Cutler | 1987 | |
| 187 255 511×2 669 1023 | |||||||||
| Notchable Unique Most Assemblies | 187 255 479 511 703 991 | 8 | 8+ | 1 / 688 | 3 | 1 | 私 (me) | 2002 | |
| 187 255 479 703 767 959 | |||||||||
| In and Out of Prison | 187 358 479 959 991 1006 | 6 | 6+ | 1 / 25 | 2 | 1 | Logan Kleinwaks | 2013 | |
| 187 614 703 887 959 991 | |||||||||
| Notchable Unique Impossible Length 10 | 187 479 511×2 887 927 | 8 | 6-8 | 1 / 64 | 4.4 | 1 | 私 (me) | 2002 | |
| 187 703 767×2 927 1006 | |||||||||
| Uranus | (189) 255 343 733 823 1023 | 4 | 6+ | 0 / 1 | 6 | 1 | 柳瀬順一 (Junichi Yananose) | 1991 | |
| (219) 255 443 686 974 1023 | |||||||||
| Abad's Level 6.7 Burr | 189 473 758 991 1022 1023 | 7 | 8+ | 1 / 25 | 6.7 | 1 | Rafael G. Abad | 2007 | |
| 219 502 697 959 1015 1023 | |||||||||
| #G | 223 447 511 831 887 895 | 9 | 6 | 1 / 102 | 6 | 1 | Peter Rösler | ||
| 191 735 767 975 1006 1007 | |||||||||
| Variation of BBB | 223 510 882 892 959 1023 | 7 | 6 | 1 / 10 | 4.2.1.2 | 1 | R. von Randow | ||
| 191 759 991 995 996 1023 | |||||||||
| Winkler's Level 3 Burr | 255×5 959 | 9 | 6 | 1 / 1 | 3 | 1 | David V. Winkler | ||
| 255×5 991 | |||||||||
| Chuck Puzzle 6 | 255×5 1023 | 10 | 6-8 | 1 / 1 | 2 | 1 | Edward Nelson | ||
| Burr in a Cage 22 | 255×4 887 1023 | 10 | 6 | 1 / 1 | 2 | 1 | 私 (me) | 2003 | max moves unique notchable with Cage Type-3 |
| 255×4 1006 1023 | |||||||||
| + Cage Type-3 | 1 / 1 | 22.1.2.2 | |||||||
| Caged Notchable 26 Moves 11 Holes | 255×4 959 1023 | 11 | 6 | 10 / 10 | 3 max | 1 | 私 (me) | 2003 | max moves notchable with Cage Type-3 |
| 255×4 991 1023 | |||||||||
| + Cage Type-3 | 8 / 10 | 26.3.1.4.2 max | |||||||
| Fossil Burr | 255×3 1022 4607 8959 | - | 6 | - | - | 1 | Yavuz Demirhan | 2014 | |
| 255×3 1015 4607 8959 | |||||||||
| + Cage | 19 | 1 / 27 | 12.2.2.2 | ||||||
| 139 Burr | 255×3 1023×3 | 14 | 10 | 7 / 11 | 1 | 1 | Bill Cutler | 1989 | |
| Susie Qube | 255×3 1023 4607 8959 | - | 8 | - | - | 1 | Yavuz Demirhan | 2017 | |
| + 6 Frames | 30 | 1 / 604 | 8.9.5.4.3.1.2 | ||||||
| Geneva | 255×2 655 767 895 1023 | 10 | 6 | 4 / 11 | 3 max | 1 | Logan Kleinwaks | 2013 | |
| 255×2 287 511 1007 1023 | |||||||||
| + Cage Type-3 | 1 / 11 | 25.2.1.4.2.2 | |||||||
| Caged Notchable Unique 12 Moves 9 Holes | 255×2 511 855 959 1006 | 9 | 6 | 7 / 12 | 3 | 1 | 私 (me) | 2003 | |
| 255×2 767 887 942 991 | |||||||||
| + Cage Type-3 | 1 / 12 | 12.2.2.4.2.2 | |||||||
| L5 Notchable | 255 326 927 959×2 991 | 7 | 6 | 1 / 30 | 5 | 1 | Bill Cutler | 1987 | |
| 255 550 927 959 991×2 | |||||||||
| Ursa Minor | 255 383 887 892 959 1015 | 9 | 6 | 4 / 4 | 2 | 1 | Jorgos Anastasou | 2023 | |
| 255 751 991 995 1006 1022 | |||||||||
| + Cage Type-3 | 1 / 4 | 13.5.2.3.22 | |||||||
| Mom | 255 443 735 767 991 1023 | 11 | 6+ | 575 / 864 | 5.2 max | 1 | Dario Uri | 2023 | |
| 255 447 511 733 959 1023 | |||||||||
| + 7/1023 | 4 | 1 / 28 | 3 | ||||||
| Blocage | 255 735 765 991 004FCF 0067DE | - | 8 | - | - | 1 | Stéphane Chomine | 2018 | |
| 255 447 507 959 002FFC 006F9E | |||||||||
| + Cage | 13 | 1 / 120 | 14.2.5.3.5.5 | ||||||
| Caged Notchable Unique Most Assemblies | 255 479 511 703 767 959 | 11 | 6 | 758 / 1,536 | 4.2 max | 1 | 私 (me) | 2003 | |
| 255 479 511 703 767 991 | |||||||||
| + Cage Type-3 | 1 / 1,536 | 5.8.2.4.2 | |||||||
| Caged Notchable Unique 6.11 Moves 11 Holes | 255 479 767×2 942 1023 | 11 | 6 | 18 / 96 | 3 max | 1 | 私 (me) | 2002 | |
| 255 511×2 703 855 1023 | |||||||||
| + Cage Type-3 | 1 / 96 | 6.11.2.1.2.2 | |||||||
| Caged Notchable Unique 6.12 Moves 11 Holes #2 | 255 511 887 910 1023×2 | 11 | 6 | 68 / 68 | 3 max | 1 | 私 (me) | 2002 | |
| 255 767 791 1006 1023×2 | |||||||||
| + Cage Type-2 | 19 | 1 / 391 | 6.12.2.1.2.2 | ||||||
| Caged Notchable Unique 6.12 Moves 11 Holes #1 | 255 511 887 1023×2 1932 | 11 | 6 | 68 / 68 | 4 max | 1 | 私 (me) | 2002 | |
| 255 767 1006 1023×2 2835 | |||||||||
| + Cage Type-2 | 19 | 1 / 312 | 6.12.2.1.2.2 | ||||||
| Caged Notchable 12.7 Moves 16 Holes | 255 511 959 1023×3 | 16 | 6 | 320 / 320 | 2 max | 1 | 私 (me) | 2002 | |
| 255 767 991 1023×3 | |||||||||
| + Cage Type-2 | 24 | 728 / 1,671 | 12.7.4.4 max | ||||||
| Caged Notchable Unique 11.5 Moves 12 Holes | 255 511 991 1006×2 1023 | 12 | 8 | 68 / 68 | 3 max | 1 | 私 (me) | 2003 | |
| 255 767 887×2 959 1023 | |||||||||
| + Cage Type-3 | 1 / 68 | 11.5.2 | |||||||
| Kubulus | 255 1023 8959×4 | - | 6 | - | - | 1 | Yavuz Demirhan | 2015 | |
| 255 1023 4607×4 | |||||||||
| + Cage Type-1 | 18 | 1 / 308 | 10.10.1.3.1.2 | ||||||
| Burr in Janus Cage | 655 703 767 967 1015 1023 | 10 | 6 | 36 / 84 | 6 max | 1 | Logan Kleinwaks | 2013 | |
| 287 479 511 830 1022 1023 | |||||||||
| + Cage Type-5 | 1 / 336 | 20.6.2.7.4 | |||||||
| Jailbreak Burr | 447 655 886 1007 1022 1023 | 9 | 6 | 9 / 16 | 3 max | 1 | William Hu | 2014 | |
| 287 735 895 998 1015 1023 | |||||||||
| + Cage Type-6 | - | 1 / 105 | 14.6.5.4.2.2 | ||||||
| Most Assemblies Unique Level 8 | 303 415 759 767 989 1023 | 8 | 10+ | 1 / 111 | 8 | 1 | Bill Cutler | 1990 | |
| 303 510 511 671 955 1023 | |||||||||
| Computer's Choice 3-Hole | 354 511 710 925 1014 1023 | 3 | 6+ | 1 / 7 | 7.1.2 | 1 | Bill Cutler | 1988 | |
| 310 612 767 923 1014 1023 | |||||||||
| TriBurr 1 | 311 379 462 615 827 927 | 0 | 6+ | 1 / 1 | 1 | 1 | Min S. Shih | 2003 | |
| 366 567 718 749 927 973 | |||||||||
| Schism | 319 511 767 886 1014 1023 | 10 | 6 | 21 / 25 | 4 max | 1 | Tim Alkema | 2017 | |
| 511 719 767 998 1014 1023 | |||||||||
| + 2 Frames | 10 | 1 / 528 | 7.8.7.4 | ||||||
| Notchable Unique 4.6 Moves Length 8 | 343 411 669 887 1023×2 | 6 | 8+ | 1 / 4 | 4.6 | 1 | 私 (me) | 2002 | |
| 411 669 686 1006 1023×2 | |||||||||
| Caged Millable 30 Moves 11 Holes #2 | 507 686 887 991 1023×2 | 11 | 6 | 137 / 144 | 3 max | 1 | 私 (me) | 2003 | |
| 343 765 959 1006 1023×2 | |||||||||
| + Cage Type-3 | 45 / 144 | 30.2 max | |||||||
| Twist-Key Burr | 358 614 910 974×2 (1023) | 0 | 6+ | 2 / 2 | 2 | 1 | Unknown | [R] |
|
| 358 614 791 823×2 (1023) | |||||||||
| Abad's Level 4 Ambiguous Burr | 358 614 927 955 991 1023 | 5 | 6+ | 1 / 80 | 4.2 | 1 | Rafael G. Abad | 2006 | |
| 358 614 927 959 989 1023 | |||||||||
| Parasitic Burr | 366 511 767 823 959 991 | 9 | 6+ | 68 / 132 | 3 max | 1 | Tyler Hudson | 2023 | |
| 511 615 767 959 974 991 | |||||||||
| + 4/8×2 | 1 | 1 / 6 | 3 | ||||||
| Computer's Choice Unique 10 | 367 475 511 996 1014 1023 | 7 | 8 | 1 / 7 | 10 | 1 | Bill Cutler | 1990 | co-max moves unique 8-len |
| 623 701 767 882 1014 1023 | |||||||||
| Computer's Choice 4-Hole | 368 870 894 927 989 1023 | 4 | 6+ | 1 / 5 | 8.3 | 1 | Bill Cutler | 1988 | |
| 368 870 927 955 999 1023 | |||||||||
| BC UL6000 | 374 447 735 767 879 1014 | 7 | 6 | 1 / 9 | 6.4 | 1 | Bruno Curfs | ||
| 447 511 735 742 879 1014 | |||||||||
| Vanity Box | 639 751 1023 4983 5111 12735 | - | 6 | - | - | 1 | Donald Osselaer | 2012 | |
| 383 495 1023 4983 9214 12735 | |||||||||
| + Cage Type-2 | 23 | 1 / 929 | 23.8.1.2.2 | ||||||
| Beauty and Poverty at the Equator | 751 753 989 1007 1023×2 | 11 | 6 | 12 / 13 | 3.2 max | 2 | Logan Kleinwaks | 2014 | |
| 383 504 895 955 1023×2 | |||||||||
| + Cage Type-3 | 1 / 13 | 31.2.2.5 | |||||||
| Notchable 10 Moves 11 Holes | 411 479 494 1023×3 | 11 | 10+ | 77 / 112 | 10 max | 1 | 私 (me) | 2002 | |
| 631 669 703 1023×3 | |||||||||
| Complex Level 5.4 Notchable Burr | 479×2 669 703 767 991 | 8 | 6 | 1 / 144 | 5.4 | 1 | David V. Winkler | ||
| 411 479 511 703×2 959 | |||||||||
| Alkippe | 506 511 669 767 886 1014 | 6 | 6 | 1 / 5 | 3.2 | 1 | Terry Smart | 2016 | |
| 411 511 757 767 998 1014 | |||||||||
| + Cage | 1 / 5 | 16.1.3.2.2 | |||||||
| + Cage | 1 / 5 | 7.2.1.1.2 | |||||||
| Caged General Unique 10 Moves 7 Holes | 639 671 989 1015 1022 1023 | 7 | 6 | 82 / 105 | 4.2 max | 1 | Jan Naert | 2006 | |
| 415 495 955 1015 1022 1023 | |||||||||
| + Cage Type-3 | 1 / 105 | 10.2.3.2 | |||||||
| Abad's Level 4.9 Burr | 443 511 671 757 879 1015 | 7 | 6 | 1 / 6 | 4.9 | 1 | Rafael G. Abad | 2006 | |
| 415 506 733 767 879 1022 | |||||||||
| Siamese Burrs | 415 511 767 991 999 1007 | 11 | 6 | 20 / 34 | 4.2 max | 1 | Terry Smart | 2017 | |
| 511 671 767 894 895 959 | |||||||||
| #C "Teuflische Verführung" | 671 767 942 991 1010 1014 | 7 | 6 | 1 / 6 | 9 | 1 | Peter Rösler | ||
| 415 511 855 959 1012 1014 | |||||||||
| Caged Millable 30 Moves 11 Holes #1 | 430 447 887 991 1023×2 | 11 | 6 | 148 / 150 | 3 max | 1 | 私 (me) | 2003 | |
| 599 735 959 1006 1023×2 | |||||||||
| + Cage Type-3 | 62 / 150 | 30.2 max | |||||||
| Abad's Level 5.7 Burr | 431 895×2 955 985 999 | 8 | 6 | 1 / 4 | 5.7 | 1 | Rafael G. Abad | 2005 | |
| 607 894 953 989 1007×2 | |||||||||
| Notchable Unique 4.6 Moves Length 6 | 443 767 870 887 927×2 | 6 | 6+ | 1 / 4 | 4.6 | 1 | 私 (me) | 2002 | |
| 511 733 870 927×2 1006 | |||||||||
| Caged Millable Unique 12.10 Moves 11 Holes | 447 511 735 927×2 1023 | 11 | 6 | 242 / 336 | 5.3 max | 1 | 私 (me) | 2003 | |
| 447 735 767 927×2 1023 | |||||||||
| + Cage Type-3 | 1 / 336 | 12.10.3.4.2.2 | |||||||
| Solid Puzzle No.4 | 460 510 567 787 919 1022 | 0 | 6+ | 1 / 1 | 1 | 1 | テンヨー (Tenyo) | ||
| 462 563 759 908 926 1015 | |||||||||
| Programmer's Nightmare | 498 701 767 989 1011 1023 | 8 | 8+ | 1 / 102 | 5.3 | 1 | Bill Cutler | 1989 | [R] |
| 475 511 756 955 1020 1023 | |||||||||
| Mega Six | 475 511 863 996 1014 1023 | 8 | 8 | 1 / 20 | 10 | 1 | Bill Cutler | 1990 | co-max moves unique 8-len |
| 701 767 882 943 1014 1023 | |||||||||
| Caged Notchable Unique 13 Moves 11 Holes | 479×2 991 1006×2 1023 | 11 | 6 | 30 / 30 | 3.2 max | 1 | 私 (me) | 2003 | |
| 703×2 887×2 959 1023 | |||||||||
| + Cage Type-3 | 1 / 30 | 13.2.2.2.2 | |||||||
| #D "Super" | 703 759 767 947 1014 1015 | 9 | 6 | 1 / 38 | 9 | 1 | Peter Rösler | ||
| 479 510 511 988 1014 1022 | |||||||||
| Queen of Sheba | 479 703 767 1023×3 | 15 | 6 | 640 / 640 | 3 max | 1 | Yavuz Demirhan | 2016 | |
| 479 511 703 1023×3 | |||||||||
| + Frame | 1 / 2,560 | 11.2.1.3.3.2 | |||||||
| Caged Notchable 13.8 Moves 16 Holes | 479 703 1023×4 | 16 | 6 | 82 / 82 | 2 max | 1 | 私 (me) | 2002 | |
| + Cage Type-2 | 24 | 173 / 518 | 13.8 max | ||||||
| Burr 5-6 | 479 823 925 991 1010 1022 | 7 | 6 | 1 / 13 | 5.6.2.2 | 1 | Andrey Ustjuzhanin | 2014 | |
| 703 923 959 974 1012 1015 | |||||||||
| Vanity Box 2 | 479 999 1023 4599 4863 4983 | - | 6 | - | - | 1 | Donald Osselaer | 2012 | |
| 703 894 1023 4983 8703 8958 | |||||||||
| + Cage Type-2 | 22 | 1 / 1,417 | 23.7.3.3.3 | ||||||
| Aubade | 479 1006 1014 1023 12795 22413 | - | 6 | - | - | 1 | Stéphane Chomine | 2017 | |
| 703 887 1014 1023 13053 24024 | |||||||||
| + Cage | 12 | 1 / 119 | 13.5.2.2.2.2 | ||||||
| Abad's Level 4.8 Burr | 483 894 943 959 985 1022 | 7 | 6 | 1 / 2 | 4.8 | 1 | Rafael G. Abad | 2005 | |
| 636 863 953 991 999 1015 | |||||||||
| Jean Mourik | 486 637 959 1014 1023×2 | 10 | 6 | 30 / 31 | 6 max | 1 | Jean Mourik | ||
| 491 630 991 1014 1023×2 | |||||||||
| Love's #1 | 487 882 895 991×2 1023 | 10 | 6 | 6 / 14 | 6.2.2 max | 1 | Bruce Love | ||
| 638 959×2 996 1007 1023 | |||||||||
| Houdini | 757 4863 8958×2 9215 13055 | - | 6 | - | - | 1 | Stéphane Chomine | 2011 | |
| 506 4599×2 5119 8703 12799 | |||||||||
| + Cage | 25 | 1 / 671 | 19.5.5.3 | ||||||
| 2 Sons | 507 511 959 1014 1020 13303 | - | 6 | - | - | 2 | Ken Johnson | 2024 | |
| 765 767 991 1011 1014 13303 | |||||||||
| + 4/5 4/8 | 5 | 1 / 6 | 4.6.3.3.2 | ||||||
| Attis | 511×2 767×2 879 991 | 13 | 6+ | 72 / 96 | 3 max | 1 | Terry Smart | 2015 | |
| 511×2 767×2 879 959 | |||||||||
| + 3 Frames | 14 | 6 | 1 / 384 | 15.14.4.1.2 | |||||
| GELO-1868 | 511×2 4159 4927 8959 12795 | - | 6 | - | - | 1 | Oleg Smol'yakov | 2021 | |
| 767×2 4383 4479 4607 13053 | |||||||||
| + Cage | 38 | 1 / 1,224 | 12.11.2.3.1.2 | ||||||
| 2-Face | 511 831 4575 5119 8703 12799 | - | 6 | - | - | 2 | Stephan Baumegger | 2016 | |
| 767 975 4863 8895 9215 13055 | |||||||||
| + Cage Type-2 | 26 | 1 / 14 | 29.2.4.1.3 | ||||||
| Nyx | 767 923 998 1007 1014 1023 | 10 | 6 | 100 / 135 | 5 max | 1 | Terry Smart | 2016 | |
| 511 886 895 925 1014 1023 | |||||||||
| + Cage | 2 / 810 | 16.2.2.2.2.2 max | |||||||
| Parasitic Version | 511 887×2 959×2 1023 | 13 | 6+ | 100 / 100 | 2 max | 1 | László Molnár | 2023 | |
| 511 991×2 1006×2 1023 | |||||||||
| + 4/6 4/7 4/8 | 1 | 1 / 15 | 3 | ||||||
| Ribbon Burr | 767 1023 4347 8959×3 | - | 6 | - | - | 1 | Yavuz Demirhan | 2015 | |
| 511 1023 4607×3 8445 | |||||||||
| + Frame | 17 | 1 / 80 | 6.4.3.2.2 | ||||||
| La Mente | 767 4383×2 4607 9215 12543 | - | 6 | - | - | 1 | Stephan Baumegger | 2014 | |
| 511 4159×2 5119 8959 12543 | |||||||||
| + Cage Type-2 | 22 | 1 / 974 | 11.13.12.1.1.3 | ||||||
| Plankton | 767 4319 4575 8959 9119 25343 | - | 6 | - | - | 2 | Stephan Baumegger | 2015 | |
| 511 4607 5023 8383 8895 29647 | |||||||||
| + Frames | 24 | 1 / 257 | 10.1.13.2.6.2.4.1.1.1.1.1.2 | ||||||
| BB31-147-1 | 789 819 887 906 1006 1022 | 1 | 6+ | 1 / 2 | 3 | 1 | Bill Cutler | ||
| 789 887 906 972 1006 1015 | |||||||||
| Bill Cutler's Bin Cross | 791 870 942 959 991 1023 | 7 | 8+ | 30 / 46 | 5 max | 1 | Bill Cutler | ||
| 855 870 910 959 991 1023 | |||||||||
| + Cage | 1 / 46 | 4.1.2 | |||||||
| BB43-143M-1 | 831 855 883 954 1004 1016 | 3 | 6+ | 1 / 2 | 4 | 1 | Bill Cutler | ||
| 883 942 975 981 1004 1009 | |||||||||
| O'Beirne's 8 Piece Burr | 887×3 1006×3 | 8 | 6+ | 2 / 2 | 1 | 1 | Thomas H. O'Beirne | ||
| + 4/4×2 | 0 | 2 / 2 | 1 | ||||||
| Vertex Burr #2 | 927 1015 1023 4607 5119 8447 | - | 6 | - | - | 2 | Yavuz Demirhan | 2012 | |
| 927 1022 1023 4351 8959 9215 | |||||||||
| + Cage Type-4 | 18 | 1 / 1 | 15.14.3.2.2.2 | ||||||
| Chateau d'If | 1014 4919 5111 8958 9215 13055 | - | 6 | - | - | 1 | Stéphane Chomine | 2011 | |
| 1014 4471 4599 5119 9214 12799 | |||||||||
| + Cage Type-2 | 25 | 1 / 3,092 | 24.5.2.4.1.3 | ||||||
| Nickel Box | 4735 5111 5119 8703 8959 12799 | - | 6 | - | - | 2 | Donald Osselaer | 2012 | |
| 4607 4863 4959 9214 9215 13055 | |||||||||
| + Cage Type-2 | 29 | 1 / 3 | 28.18.17.1.1.3 | ||||||
| Circuit | 5055 6399 12539 13311×2 25343 | - | 6 | - | - | 1 | Tim Alkema | 2017 | max moves with Cage Type-1 & Type-2 |
| 9183 9471 12541 13311×2 29647 | |||||||||
| + Cage Type-1 | 24 | 1,415 / 13,133 | 24.3 max | ||||||
| + Cage Type-2 | 32 | 2,704 / 13,133 | 40.11.11.1.1.3 max | ||||||
| Iron Maiden | 000F9F 002E9F 00479F 004F9F 00679F 006F9F | - | 8 | - | - | 2 | Alfons Eyckmans | 2011 | |
| 0007FE 0027BE 0027FE 0045FE 0067BE 0067FE | |||||||||
| + Cage | 19 | 1 / 1,536 | 22.13.5.4.2.2 | ||||||
| Burr Prisoner #1 | 008FBE 00CCBF 10B1DF×2 10F0DF 10FCFF | - | 8 | - | - | 1 | Stéphane Chomine | 2014 | |
| 0017DF 0034FF 1017DF 1035DF×2 20FCFF | |||||||||
| + Cage Type-2 | 41 | 1 / 1,352 | 28.2.3.2.1.2 | ||||||
| Aceso | 0047DF 006FBE 00E35F 1607DF 16605F 1E66C1 | - | 8 | - | - | 1 | Terry Smart | 2015 | |
| 002FBE 0067DF 007B3E 16035F 16F05F 1ED341 | |||||||||
| + Cage | 29 | 1 / 24 | 16.1.1.1.3 | ||||||
| Cube Burr A | 0064DF 009DFF 00C4DF 00FB7F 1007DF 1017C3 | - | 8 | - | - | 1 | Olexandre Kapkan | 2014 | |
| 003CBE 006CBE 009EFF 00FB7F 10F05F 10F0C3 | |||||||||
| + Cages Type-2 | 35 | 1 / 52 | 21.1.3.1.2 | ||||||
| Burr Prisoner #2 | 00AFB6 00F9FF 10F25B 10F2DB 20EDFF 20FDFF | - | 8 | - | - | 3 | Stéphane Chomine | 2014 | |
| 0057DB 00FE7F 1047DB 1057DB 107EFF 10FEFF | |||||||||
| + Cage Type-2 | 47 | 1 / 420 | 36.1.2.2.2 | ||||||
| Half Burrow | 0067DF×2 00FB3E×2 1007DF 16F05B | - | 8 | - | - | 1 | Alexander Magyarics | 2022 | |
| 006FBE×2 00F35F×2 10F05F 1607DB | |||||||||
| + 3 Cages | 29 | 1 / 36 | 12.9.1.6.4.2.2.5 | ||||||
| Cube Burr D | 006FBE 1014DF 1017D3 1034DF 10D0DF 200FFE | - | 8 | - | - | 1 | Olexandre Kapkan | 2014 | |
| 0067DF 100FDF 1016DF 1090DF 1091DF 10F0D3 | |||||||||
| + 2 Cages | 34 | 1 / 576 | 22.1.5.1.2 | ||||||
| Cube Burr B | 00EFBF 00F87F 100EFF 10597F 111E3E 209B7F | - | 8 | - | - | 1 | Olexandre Kapkan | 2014 | |
| 0077FF 00F87F 109B7F 200DFF 20AA7F 21C0FE | |||||||||
| + 2 Cages | 33 | 1 / 2 | 9.4.2.2.5.4 | ||||||
| Penitencier | 00EDFE 105FDF 10C87F 20D7FF 20F9FF×2 | - | 8 | - | - | 1 | Stéphane Chomine | 2018 | |
| 007EDF 10BFBF 10FE7F×2 20387F 20AFFE | |||||||||
| + Cage | 45 | 1 / 3,285 | 45.8.5.3.3.4 | ||||||
| Eclisse | 00BFFF 10F5FF 20B7FF 20FCF7 302FFF 304FFF | - | 8 | - | - | 2 | Stéphane Chomine | 2018 | |
| 00DFFF 10B7FF 10DFBF 10FCFB 302FFF 304FFF | |||||||||
| + 2 Cages | 48 | 1 / 1,904 | 37.1.1.1.9.2.2 | ||||||
| Cube Burr A Hard | 00F05F 101EFF 109DFF 10F0D3 10FA7F 2099FF | - | 8 | - | - | 1 | Olexandre Kapkan | 2014 | |
| 00F83E 1017D3 109E7F 208DFF 209EFF 20F97F | |||||||||
| + Cages Type-2 | 42 | 1 / 1,058 | 30.1.5.3.2 | ||||||
| Reign | 00FEFF 109F9F 10FAFF 238FFF 306FFF 608FFF | - | 8 | - | - | 1 | Dan Fast | 2015 | |
| 00FDFF 1C1FFF 2097FE 20FD7F 306FFF 70FC3F | |||||||||
| + Cage | 53 | 1 / 8,176 | 40.7.18.3.2 | ||||||
| Ben | 041FFF 20EFFE 32EC7F 53FC1F 5F7C27 70FE3F | - | 8 | - | - | 1 | Stephan Baumegger | 2018 | |
| 014FFF 107FDF 328F7F 57F9F0 5F37F0 60CFFF | |||||||||
| + Cage | - | 1 / 282 | 36.6.3.2.2 | ||||||
| Cube Burr C | 10165F 1091DF 1098FF 109DFF 10F87F 306FFF | - | 8 | - | - | 1 | Olexandre Kapkan | 2014 | |
| 1034DF 10C0DF 209C7F 209EFF 20F87F 306FFF | |||||||||
| + 2 Cages | 44 | 1 / 1,680 | 23.3.5.4 | ||||||
| Penitencier #2 | 10FD7F×6 | - | 8 | - | - | 1 | Stéphane Chomine | 2018 | |
| 20FAFF×6 | |||||||||
| + Cage | 53 | 1 / 213 | 27.10.7.4.3.5 |
|
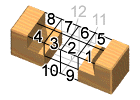駒の番号は、右図の12箇所のどこが欠けているか(Notch)を示している。右図の数字は 2進数の桁位置で、000000000000b は全く欠けていないことを表わす。1と5が欠けている駒は、000000010001b で、これは 17番である。4と8が欠けている駒は 000010001000b で 136番であるが、回転すれば 17番と同じであり、より小さい番号が採用される。
この番号付けの規則は、Cutler のものと若干異なっているが、本質的には同じ。
0番～4095番のうち、左右に分離せずに繋がるものは 837駒ある。そのうち、Notchable が 59駒、Millable が 19駒。
Burrs Catalogue にすべての駒のカタログがある。
切り欠きは単位立方体とするのが普通であるが、半単位にしたり、斜めにしたりする変形もある。
すべての切り欠き(Notch)が端から端まで達している駒 (上の表のこの色の駒)。
この駒は刃の幅１ののこぎりがあれば作れる。
Notchable ではないが、3面を残した切り欠きのない駒 (上の表のこの色の駒)。
名前は、ミル(milling machine)で加工可能なことから。
Notchable でも Millable でもない駒 (上の表のこの色の駒)。
無垢材から切り出すのは面倒。
6本組木の組み上がり時の交差部分は以下のようになる。このとき、切り欠き(Notch)は外からは見えない O に位置させることが要求される。これが組み上がり状態での穴となる。
...... | ...... | .XXXX. | .XXXX. | ...... | ...... ..XX.. | ..XX.. | .XOOX. | .XOOX. | ..XX.. | ..XX.. ..XX.. | XXOOXX | XOOOOX | XOOOOX | XXOOXX | ..XX.. ..XX.. | XXOOXX | XOOOOX | XOOOOX | XXOOXX | ..XX.. ..XX.. | ..XX.. | .XOOX. | .XOOX. | ..XX.. | ..XX.. ...... | ...... | .XXXX. | .XXXX. | ...... | ......
可能な最大の穴の数は 20。
穴のない駒組みは Solid Burr と呼ばれ、Notchableな駒による構成での分解可能な組み合わせが 221通り、314解あることが Cutler により求められている。
このとき使用されるNotchableな駒は25種で、これらの駒を特別扱いすることがある。これらの駒を Notchable32 Burr と呼ぶことがある(von Känel)。この32は、上図の32箇所の O がすべて埋まっていることに由来する。
穴のある駒組みは Holey Burr である。
穴を外から見える所に位置させてもよいとする組み方もある。
上の表で + Cage とあるものは枠内に組むもの (Caged Burr) で、移動に制約があり、裸の状態よりも分解可能な組み合わせの数は少なく、分解手順も異なる。枠の形状にはいくつかある。Type-1 ～ 3 は、6×6×6 を単純に穿ったものと、隅の 2×2×2 を削ってすべて厚さ1にしたもの、枠だけのものである。 Type-1、Type-2 の枠の場合は、穴の位置がまったく見えないので、穴を外側に位置させても構わないであろう。
 |
XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX XX..XX | XX..XX | X....X | X....X | XX..XX | XX..XX XX..XX | ...... | ...... | ...... | ...... | XX..XX XX..XX | ...... | ...... | ...... | ...... | XX..XX XX..XX | XX..XX | X....X | X....X | XX..XX | XX..XX XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX |
 |
XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX XX..XX | X....X | X....X | X....X | X....X | XX..XX XX..XX | ...... | ...... | ...... | ...... | XX..XX XX..XX | ...... | ...... | ...... | ...... | XX..XX XX..XX | X....X | X....X | X....X | X....X | XX..XX XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX |
 |
XXXXXX | X....X | X....X | X....X | X....X | XXXXXX X....X | ...... | ...... | ...... | ...... | X....X X....X | ...... | ...... | ...... | ...... | X....X X....X | ...... | ...... | ...... | ...... | X....X X....X | ...... | ...... | ...... | ...... | X....X XXXXXX | X....X | X....X | X....X | X....X | XXXXXX |
 |
XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX XX..XX | X..... | X..... | X..... | X..... | X..... XX..XX | ...... | ...... | ...... | ...... | X..... XX..XX | ...... | ...... | ...... | ...... | X..... XX..XX | X..... | X..... | X..... | X..... | X..... XXXXXX | X..... | X..... | X..... | X..... | X..... |
 |
XXXXXX | XXXXXX | X....X | X....X | XXXXXX | XXXXXX XX..XX | X..... | X..... | X..... | X..... | X....X XX..XX | ...... | ...... | ...... | ...... | X....X XX..XX | ...... | ...... | ...... | ...... | X....X XX..XX | X..... | X..... | X..... | X..... | X....X XXXXXX | X....X | X....X | X....X | X....X | XXXXXX |
 |
XXXXXX | X.XX.X | X....X | X....X | X.XX.X | XXXXXX X....X | ...... | X....X | X....X | ...... | X....X XX..XX | ...... | ...... | ...... | ...... | XX..XX XX..XX | ...... | ...... | ...... | ...... | XX..XX X....X | ...... | X....X | X....X | ...... | X....X XXXXXX | X.XX.X | X....X | X....X | X.XX.X | XXXXXX |
Bill Cutler's Bin Cross の枠はこれらとは異なり、駒の長さは 8以上必要。
駒の長さは、6単位以上の偶数単位が普通である。長さが異なると解き方の異なる駒組が多数存在する。12単位以上は 12単位と等価である(たぶん)。例えば 8+ と表記されているものは 8単位以上で解き方に違いがないことを示す。6+ は長さ非依存である。
組み上がり状態から何手で駒が外れていくのかを示す。4.2.1.1 ならば、最初の駒が外れるのに 4手、次の駒が外れるのに 2手、次と次は 1手要することを示す。何駒が同時に外れるのかはこれからはわからない。一度に複数駒外れることもある。1手は直ちに外れるということで、後行する .1 の連続は省略して 4.2 などと表記する。
ここで言う 1手は、同一の駒の組が同一方向に同一単位移動するのを 1手と勘定する。ただし、移動は軸に沿った平行移動に限る。L字型の移動は 2手である。
一部には分解に回転を要するものもある。回転は、同一軸の周りに同一方向に同一角の回転を 1手とする。
同時に複数の駒が外れる場合、それは 2ないし3駒である。それらの分かれた駒組の分解がすべて 1手で済むのなら、それを表現する必要はない。仮に、5手で 4 + 2 に分かれた後、4駒の分解が 3.2、2駒の分解が 1手であれば、これは 5.3.2 と表現してよい。もし、2駒の分解に 2手を要する場合は、5.(3.2+2) などと表現する(予定は未定)。
同じ組み方で異なる外し方が存在する場合は、より少ない手数で外れていく方を採用する。4.2 よりも 2.1.4 を採用する。これは、最後の 1駒になるまでの総手数の少ない方ではない。最初の駒の外れるのに要する手数の少ない方である。最初が同じなら次の駒の手数の少ない方。最初が同じでも、外れる駒数が異なる場合にどうするかは未定。
1回の移動で、一部の駒が外れて他が外れずに残ることもあり得る。それは移動に 1手、外すのに 1手と勘定する。
Bill Cutler は、同一軸方向への移動は、移動量が異なったり逆方向であっても 1手と勘定し、これを Level
と称して、駒組の難易度の指針とした。この 1手の定義は、あまり直感的でない(と私には思える)。ここでは Level は採用しなかった。
Cutlerらの命名に、L5 などとあるのは、Level 5 のことであり、ここで示している手数とは違っている可能性もあるが、Level と Moves が食い違うのはそう多くはない。ここに挙げてあるものの中では、例えば次が食い違っている。
| Moves | Level | |
| Computer's Choice 4-Hole | 8.3 | 7.2 |
| Burr 'A' | 5 | 4 |
| Love's #1 | 6.2.2 | 5 |
分母は、分解不可能なものも含めての組み上げ方の総数を示し、分子は、そのうち平行移動だけによる分解可能な解の数を示す。
分母は Length によらないが、分子は Length に依存する。
分子が 0 となっているものは、平行移動だけでは解けないことを示すが、Moves が 0 でないものはその手数で解けることを意味する。ではどうやって解くのかといえば、回転操作を含んだり、駒に細工があったり、それぞれのデザイナの智恵が詰まっている。